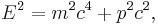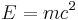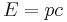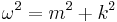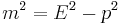Energy–momentum relation

In special relativity, the energy-momentum relation is a relation between the energy, momentum and the mass of a body:

E^2 = m^2 c^4 %2B p^2 c^2 , \;

where c is the speed of light, 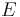E \; is total energy, 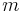m \; is invariant mass, and 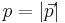p = |\vec p|\; is momentum.

For a body in its rest frame, the momentum is zero, so the equation simplifies to

E = mc^2 \;

If the object is massless then the energy momentum relation reduces to

E = pc \;

as is the case for a photon.

In natural units the energy-momentum relation can be expressed as

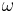\omega^2 = m^2 %2B k^2 \;

where \omega \; is angular frequency, 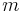m \; is rest mass and 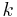k \; is wave number.

In Minkowski space, energy and momentum (the latter multiplied by a factor of c) can be seen as two components of a Minkowski four-vector. The norm of this vector is equal to the square of the rest mass of the body, which is a Lorentz invariant quantity and hence is independent of the frame of reference.

When working in units where c = 1, known as the natural unit system, the energy-momentum equation reduces to

m^2 = E^2 - p^2 \,\!

In particle physics, energy is typically given in units of electron volts (eV), momentum in units of eV/c, and mass in units of eV/c2. In electromagnetism, and because of relativistic invariance, it is useful to have the electric field E and the magnetic field B in the same unit (gauss), using the cgs (gaussian) system of units, where energy is given in units of erg, momentum in g.cm/s and mass in grams.

Energy may also in theory be expressed in units of grams, though in practice it requires a large amount of energy to be equivalent to masses in this range. For example, the first atomic bomb liberated about 1 gram of heat, and the largest thermonuclear bombs have generated a kilogram or more of heat. Energies of thermonuclear bombs are usually given in tens of kilotons and megatons referring to the energy liberated by exploding that amount of trinitrotoluene (TNT).

See also